Nous allons voir comment réaliser une ANOVA lorsque nos données concernent différents échantillons (plus de 2). Pour cela, nous allons utiliser R (avec Excel, il n’est possible de faire une ANOVA qu’avec 2 échantillons différents).
ANOVA signifie Analyse Of Variance. C’est un test basé sur le test de Fisher (pour les variances) qui vérifie si la moyenne de différents échantillons/groupes est différente, en tenant compte de la variance de chaque échantillon/groupe.
Avant de faire une ANOVA
Il faut s’assurer que les données suivent une loi normale et que la variance des échantillons est homogène, comme pour le t-test.
- Pour vérifier la normalité des données, le test de normalité de Shapiro-Wilk ou un Q-Q plot peut être réalisé
- Pour vérifier l’homogénéité des variances, le test F de Fischer-Snedecor peut être réalisé
Avec R, il faut que les données soient structurées comme dans une base de données. C’est à dire que les mesures des différents échantillons sont mises les unes en-dessous des autres (lignes différentes), et non dans des colonnes différentes ce qui signifierait qu’il s’agit de variables différentes. La différence entre les échantillons est donc contenue dans une variable qui sera considéré comme un facteur (il s’agit d’une variable qualitative avec des données textuelles pour différencier les groupes/échantillons).
L’Anova se base sur un modèle linéaire qu’il faut préalablement définir. On peut définir différents modèles selon la situation qu’on souhaite analyser. Les principales différences concernent les points suivants :
- Le nombre de facteurs (variables qualitatives). A ne pas confondre avec les échantillons, les facteurs sont des variables permettant de différencier les échantillons (par exemple l’âge ou le sexe)
- L’interaction entre différents facteurs.
Si il n’y a qu’1 seul facteur, on parle de One-way ANOVA.
Le modèle linéaire à établir est le suivant : lm(variable~facteur,data=données)
Si il y a 2 facteurs, on parle de Two-way ANOVA (ou MANOVA), on teste alors l’effet de ces 2 facteurs en même temps. On peut modéliser unt Two-way ANOVA de 2 facons : si il y a ou non une interaction entre les facteurs.
Si il y a une interaction, le modèle est le suivant : lm(variable~facteur1*facteur2,data=données)
Si on considère qu’il n’y a pas d’interaction, le modèle est le suivant : lm(variable~facteur1+facteur2,data=données)
Faire l’ANOVA avec R
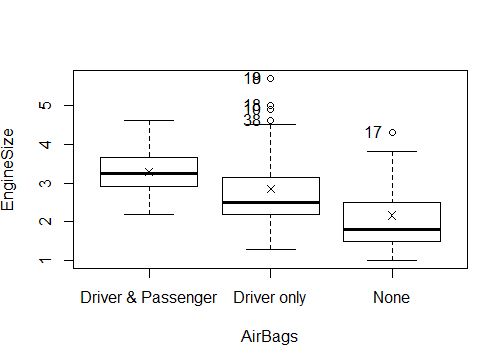
Nous allons montrer un exemple d’ANOVA que nous allons réaliser avec la base de données cars93 dans R. Cette base de données contient le prix de base de différents véhicules automobiles, ainsi que leur catégorie (petite, grande, compacte, sportive, van, etc).
Un t-test ne conviendrait pas car il y a plus de 2 échantillons/groupes (plus de 2 catégories de véhicules).
Nous allons réaliser une ANOVA pour savoir si le prix des voitures est le même entre les différentes catégories. Il s’agit donc d’une One-way ANOVA (un seul facteur utilisée : la catégorie de véhicule).
Nous définissons le modèle à utiliser pour l’ANOVA de la sorte :
lm( Min.Price ~ Type , data=Cars93 )
, ce qui correspond à : Prix de base ~ Catégorie de véhicule
A noter : il existe 2 fonctions similaires pour faire une ANOVA avec R : aov() et anova()
- Avec aov(), le modele peut-être directement renseigné en argument et le résultat s’affiche en éxécutant la fonction summary() de l’objet résultant de aov(). Ce qui donne : > testanova <- aov(Min.Price~Type,data=Cars93) , puis > summary(testanova)
- Avec anova(), il faut préalablement construire le modèle avec la fonction lm() et ensuite utiliser l’objet contenant ce modèle dans la fonction anova() qui affiche les résultats du test. Ce qui donne : > modele <- lm(Min.Price~Type,data=Cars93), puis > anova(modele)
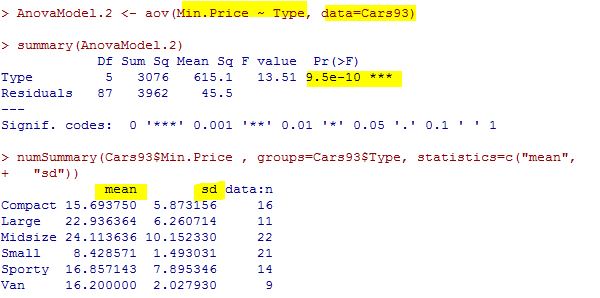
Nous allons maintenant regarder les résultats de l’ANOVA ci-dessous :
On constate que la p-value pour le facteur « Type » est inférieure à 0,05. Ce qui fait qu’on peut rejeter l’hypothèse nulle d’égalité des moyennes entre les groupes de ce facteur.
Il y a donc une différence avec le facteur « type », ce qui signifie que les prix de base ne sont pas les mêmes selon les catégories de véhicules.
En regardant le descriptif des différents groupes de catégorie de véhicules, on a une idée des différences (certaines moyennes sont éloignées, cependant étant donnée les écart-type, on ne peut pas affirmer avec certitude que telle catégorie de véhicule est différente d’une autre).
Identifier d’où vient une éventuelle différence
Maintenant que nous savons qu’il y a une différence en termes de prix entre les catégories, il est intéressant de connaitre quelles catégories de véhicules différent (est-ce que toutes les catégories sont différentes ? ou uniquement certaines ?)
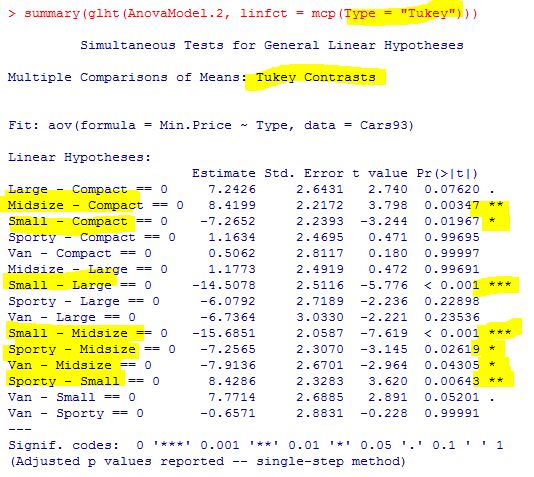
Pour cela nous allons réaliser le test de Tukey qui permet de comparer les moyennes de chaque catégorie 2 à 2. Le test va se faire en prenant un indice de confiance standart (95%).
Les résultats du test sont ci-dessous :
On constate que les différences viennent de 7 combinaisons. Les 7 autres combinaisons ont des moyennes similaires. Ainsi, la catégorie « compact » est différente de « small » et « midsize », mais les catégories « large » et « midsize » ont des prix quasiment identiques.
Pour + d’infos :
–Video d’un exemple d’ANOVA avec R
–Differences entre Anova One-way et Two-way avec Repeated measures ou non