Visualiser la distribution d’une série de données peut être utile pour avoir un premier aperçu des données, avant de faire des tests statistiques. Ceci peut se faire avec un graphique de distribution appelé box plot ou boites à moustaches.
Un box plot représente les différentes caractéristiques d’une distribution :
- La moyenne
- La médiane
- Les quartiles
- Les points extrêmes
La moyenne représente le point d’équilibre des données (le centre) en prenant en compte les valeurs de chaque donnée, ce qui fait qu’elle est sensible aux valeurs extrêmes. Contrairement à la médiane qui représente la valeur qui partage les données en 2 parties égale (50% d’un côté et 50% de l’autre).
Un quartile représente se situe au quart des données (25%). La médiane est un quartile particulier dans la mesure où il correspond au 2eme quartile (50%=25%+25%). Le premier quartile se situe au niveau où 25% des données sont en-dessous de lui et 75% au-dessus. De même le troisième quartile partage les données de telle sorte que 75% des données sont en-dessous et 25% sont au-dessus.
Les points extrêmes se déterminent à l’aide de l’écart interquartile. L’écart interquartile est la différence entre le 3eme quartile et le 1er quartile. Les points extremes sont ceux dont la valeur est inférieure à 1,5 fois l’écart interquartile en partant du 1er quartile (et supérieure à 1,5 fois l’écart interquartile en partant du 3eme quartile). On multiplie l’écart interquartile par 1,5 car cela regroupe 99,3% des données pour une distribution normale.
Comment faire un boxplot avec R Commander ?
Avant de faire le boxplot, nous allons visualiser toutes les données sur un graphiques de points (dotchart).
En prenant le set de données « Cars93 », nous allons nous intéresser à la variable « EngineSize » pour laquelle nous allons faire le dotchart représentant toutes les valeurs.
> data(Cars93, package= »MASS »)
> dotchart(sort(Cars93$EngineSize))
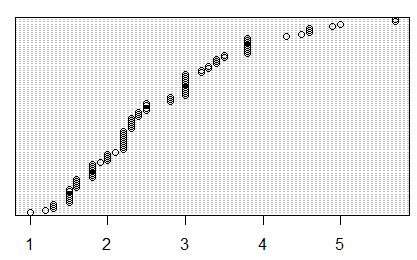 Avec ce graphique, on visualise les 93 valeurs, et on apercoit qu’une grande majorité de valeurs est entre 1,5 et 3.
Avec ce graphique, on visualise les 93 valeurs, et on apercoit qu’une grande majorité de valeurs est entre 1,5 et 3.
Ce graphique donne un premier aperçu sans donner de valeurs « repères » comme la moyenne, les quartiles ou la médiane qu’on retrouve sur un boxplot.
Pour faire un boxplot, il est possible de passer par le menu de Rcommander Graphe > Boite de dispersion.
Une fenêtre s’ouvre alors :
 Il est possible de faire automatiquement des boxplots pour chaque groupe de données (« Graphe par groupe »), c’est à dire par exemple un boxplot de la variable EngineSize selon l’équipement en Airbags.
Il est possible de faire automatiquement des boxplots pour chaque groupe de données (« Graphe par groupe »), c’est à dire par exemple un boxplot de la variable EngineSize selon l’équipement en Airbags.
Le code généré est le suivant :
> boxplot(EngineSize~AirBags, data=Cars93, id.method= »y »)
Le boxplot classique ne comprend pas la moyenne, il faut donc écrire les 2 lignes de code suivantes pour l’ajouter au graphique (croix sur le graphique) :
> tapply(Cars93$EngineSize, Cars93$AirBags,mean) -> a
> points(a,pch=4)
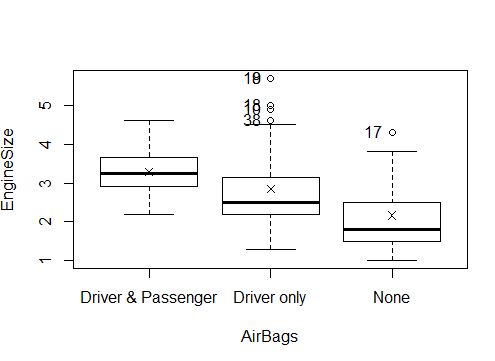 Sur les boxplot, on a plusieurs informations qui vont nous servir pour étudier ces données (les données de la variable « EngineSize » en prenant en compte les groupes Airbags avec la variable textuelle correspondante) :
Sur les boxplot, on a plusieurs informations qui vont nous servir pour étudier ces données (les données de la variable « EngineSize » en prenant en compte les groupes Airbags avec la variable textuelle correspondante) :
- Concernant les groupes : Le groupe « Airbags Driver & Passenger » a la moyenne et la médiane la plus haute, mais la différences n’est pas énorme. On observe une différence qui pourrait être étudiée entre le groupe « Airbag Driver & Passenger » et « Airbag None » étant donné que les boxs ne se « superposent pas » (en d’autres mots, le 1er quartile du groupe « Airbags Driver & Passenger » est supérieur au 3eme quartile du groupe « Airbags None »)
- Concernant le décalage entre moyenne et médiane : on observe que le décalage est plus important pour les groupes « Airbags Driver only » et « Airbags None », ce qui suggère qu’une plus grande partie des points est éloigné de la médiane (la distribution est moins concentrée). Ce fait se remarque également avec la taille de la box (plus les données sont dispersées, plus l’écart interquartile est grand).
- Concernant les points extremes : il y en a surtout pour le groupe « Airbags Driver only ». Et ces points extrêmes sont tous dans l’extrémité supérieure.
A noter : pour les quartiles, il existe plusieurs manières pour les calculer (choix de la valeur entière la plus proche, interpolation linéaire, pondération, en fonction du type de données : discrètes ou continues).
Pour + d’infos :
– Présentation du calcul classique des quartiles

2 commentaires sur “Comment visualiser une distribution avec des box plots ?”
Bonjour, le code ci-dessous ne marche pas. La ligne d’erreur me met: [19] ERREUR: impossible de trouver la fonction « Points ».
> tapply(Cars93$EngineSize, Cars93$AirBags,mean) -> a
> points(a,pch=4)
Je suis sur R commander et ai vraiment besoin de cette moyenne sur mon box-plot.
Bonjour Chanavat,
Le message précise que R ne connait pas la fonction « Points() ».
Pour corriger cette erreur, il y a 2 choses à vérifier :
– La fonction à appeler est la fonction points() tout en minuscules, c’est différent de Points() pour R
– Cette fonction est dans la librairie « graphics » qui est normalement inclus par défaut dans les installations de R. Si ce n’est pas le cas, il faut installer le package graphics et l’appeler avec le code suivant : library(graphics)