Pour répondre à certaines questions, il peut être nécessaire de réaliser des tests statistiques. Ces tests permettent, à partir d’échantillons, d’affirmer ou rejeter une hypothèse selon un degré de certitude choisi (souvent on prend la probabilité d’avoir raison dans 95% des cas). Cependant pour qu’un test statistique soit fiable, les données doivent satisfaire certaines conditions.
L’objectif de cet article est de lister certaines conditions afin de déterminer le test correspondant. Les tests présentés sont des tests basiques pour 1 ou 2 échantillons.
Les éléments à prendre en compte sont les suivants :
- La question qu’on se pose
- Les échantillons à partir desquels on a récolté des données
- Le type de données récoltées (variables)
La question qu’on se pose
Il y a généralement 2 types de questions :
-Pour savoir si deux échantillons sont similaires. En d’autres mots, est-ce qu’ils font partie de la même population ? Est-ce que les échantillons ont des caractéristiques différentes pour une même variable ? Ont-ils la même moyenne et variance ?
– Pour savoir si il y a des liens entre des variables. En d’autres mots, est-ce que les variables sont indépendantes ou non ? Est-ce que l’évolution d’une variable change la valeur d’une autre variable ?
Dans le premier cas, on se concentre sur les échantillons (en prenant une variable pour identifier des différences), alors que dans l’autre cas, ce sont les facteurs mesurés qui nous intéressent (on regarde les liens entre plusieurs variables).
Les échantillons et la population
Les échantillons correspondent à la facon dont on va effectuer les mesures, et les groupes d’individus/mesures qui doivent être différenciés.
Il y a différents tests selon le nombre d’échantillons (1 échantillon, 2 échantillons ou plus). Et dans certains cas, il faut savoir si l’échantillon est représentatif ou non de la population (si ses paramètres, comme la moyenne et la variance, sont les mêmes que ceux de la population)
De plus, il faut distinguer les observations où l’expérience est répétée avec le même échantillon (les mêmes individus), c’est à dire que 2 mesures différentes sont réalisées avec le même échantillon. On parle d’observations pairées.
Le type de données
Il existe différents types de données :
- Parmi les variables quantitatives/numériques : les données continues
- Parmi les variables quantitatives/numériques : les données discrètes
- Parmi les variables qualitatives/textuelles : les données ordinales
- Parmi les variables qualitatives/textuelles : les données nominales
Les données numériques s’opposent aux données textuelles qui ne font pas référence à des chiffres.
La différence entre une donnée continue et une donnée discrète réside dans le nombre de valeurs entre 2 valeurs . Il peut y avoir un nombre infini entre 2 valeurs continues, alors qu’entre 2 valeurs discrète, le nombre de valeurs possibles est limité.
Une donnée numérique peut devenir textuelle si on associe une valeur textuelle à un ordre de grandeur numerique ( par exemple : moins de 10 ventes = mauvais, entre 10 ventes et 20 ventes = moyen, plus de 20 ventes = bon). Cela correspond à des données catégoriques. On parle aussi de données ordinales, ce sont des données textuelles suivant une certaine hiérarchie, contrairement aux données nominales (par exemple : le sexe d’une personne est une donnée nominale). Parmi les données catégoriques, les données ordinales peuvent devenir numériques, alors que les données nominales ne sont que textuelles.
Quel test faire ?
Nous allons voir quel test statistique est adapté à quelle situation.
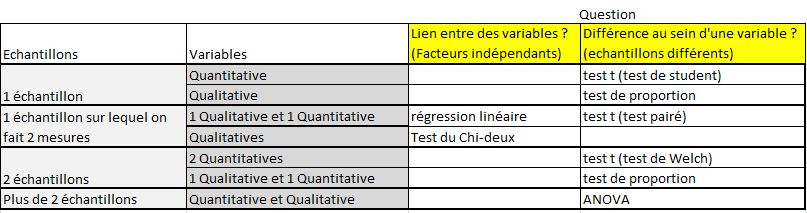
Si la question est de savoir si 1 échantillon est différent d’une moyenne, si on a qu’un seul échantillon ,et si les données sont catégoriques, alors un test de proportion convient.
Si la question est de savoir si les échantillons sont différents, si on a 2 échantillons ou plus, et si les données sont catégoriques et numériques, alors un test de proportion convient (différence de proportion).
Si la question est de savoir si deux facteurs sont indépendants, si on a qu’un seul échantillon sur lequel on effectue 2 mesures, et si les données sont catégoriques, alors un test du Chi-deux convient.
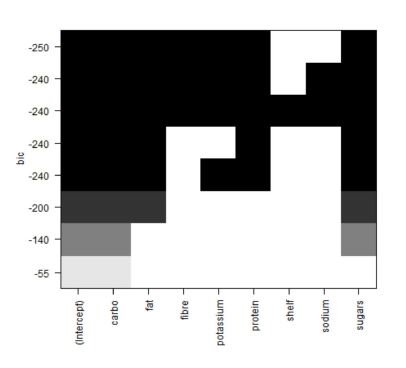
Si la question est de savoir si deux facteurs ou plus sont indépendants, si on a qu’un seul échantillon sur lequel on effectue 2 mesures ou plus, et si les données sont numériques et/ou catégoriques, alors une régression linéaire convient (incluant une table de corrélation et/ou le coefficient de détermination).
Si la question est de savoir si 1 échantillon est différent d’une moyenne, si on a 2 échantillons, et si les données sont numériques et catégoriques, alors un test t de Student convient.
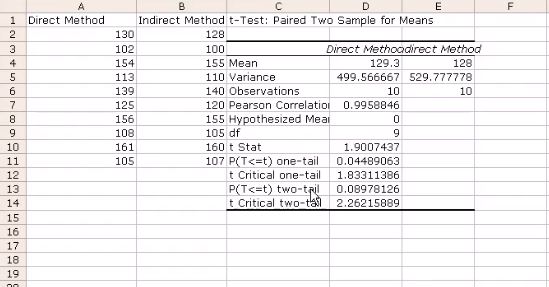
Si la question est de savoir si 2 échantillons sont différent, si on a 1 échantillon sur lequel on effectue 2 mesures, et si les données sont numériques et catégoriques, alors un test de Student pairé convient.
Si la question est de savoir si 2 échantillons sont différents, si on a 2 échantillons, et si les données sont numériques et catégoriques, alors un test t de Welch convient (ou un test t de Student, ou un z-test si on connait les variances des échantillons).
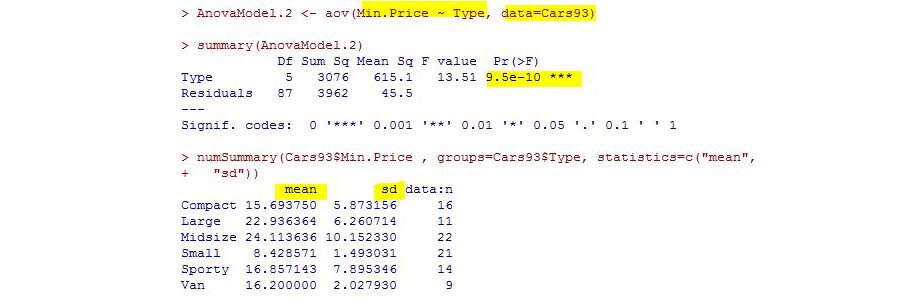
Si la question est de savoir si des échantillons sont différents, si on a 2 échantillons ou plus, et si les données sont numériques et catégoriques, alors un test ANOVA convient.
Avant d’appliquer un test, il faut aussi vérifier certaines conditions propres à chaque test, comme par exemple la condition de normalité (les échantillons suivent une loi normale) ou d’égalité des variances (variances des échantillons), etc.
Comment interpréter les resultat des tests statistiques ?
Lorsqu’on réalise un test statistique, le résultat est exprimé en fonction de l’hypothèse de départ.
On parle d’hypothèse nulle (H0). Elle correspond à une propriété non vérifiée dont le contraire peut être prouvé. Par exemple, si on fait l’hypothèse que tous les hommes ont les yeux foncés, ca peut être contredit par les hommes qui ont des yeux bleux clairs (donc tous les hommes n’ont pas les yeux foncés). Le plus souvent l’hypothèse nulle part du principe qu’il n’y a pas d’effet ou que des échantillons sont similaires (l’équation correspond donc à une égalité).
A partir de cette hypothèse, la probabilité de se tromper est calculée (on parle aussi de signification). Pour la calculer, on prend en compte l’erreur alpha qui correspond au degré d’erreur qu’on accepte (généralement 5%). Le test va alors calculer la probabilité de rejeter à tort l’hypothèse nulle. Cette p-value correspond à la probabilité de considérer que l’hypothèse est fausse, alors qu’elle peut être vraie. Ainsi si la probabilité est en-dessous de 5% (le taux d’erreur accepté), on considère qu’il est prouvé que l’hypothèse nulle est fausse (car en disant cela, on aurait raison dans plus de 95% des cas, ce qu’on considère comme un taux fiable).
Attention, si on a une p-value supérieure à 5%, cela ne signifie pas forcément qu’il n’y a pas d’effet. Il faut l’interpréter en se disant que le taux d’erreur est trop élevé (ou que le taux de fiabilité n’est pas assez élevé).
Pour + d’infos :