Lorsqu’on réalise une analyse factorielle, on simplifie la représentation du jeu de données à partir de dimensions. Ceci permet de mieux expliquer les choses en se concentrant sur l’essentiel. Le principe de l’analyse factorielle revient à avoir une vue d’ensemble avant de rentrer dans les détails (si nécessaire). Cette simplification peut également servir comme base de travail pour simplifier la représentation d’une population (des individus). On parle alors de classification.
Nous allons allons voir comment faire une classification avec R Commander. Cet exercice va se faire en partant de l’analyse en composante principale réalisée sur le jeu de données « decathlon ».
Configuration de la classification
Lors de la configuration de l’ACP, une option existe pour réaliser une classification en même temps. Il s’agit du bouton « Réaliser une classification après l’ACP ».
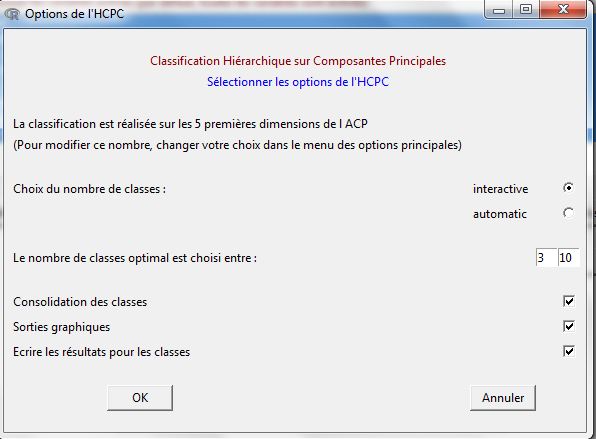
![]() En cliquant sur ce bouton, une fenêtre s’affiche permettant de sélectionner les résultats à afficher et surtout l’intervalle du nombre de classes souhaitées.
En cliquant sur ce bouton, une fenêtre s’affiche permettant de sélectionner les résultats à afficher et surtout l’intervalle du nombre de classes souhaitées.
Une fois l’ACP et la classification lancée, un premier graphique s’affiche.
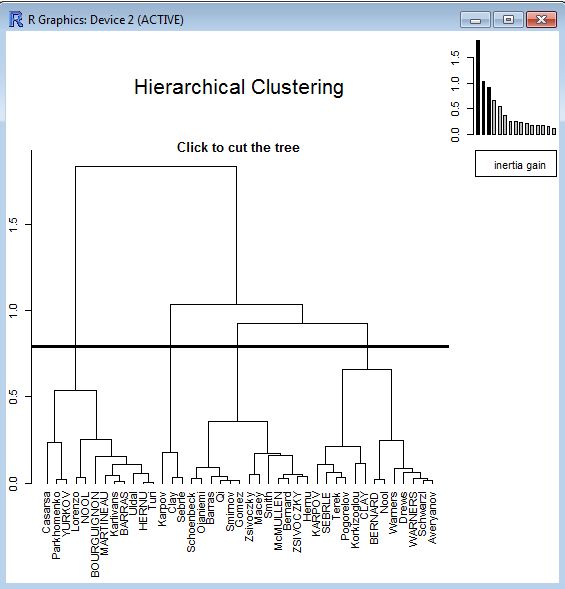
Il s’agit du graphique de la classification sous la forme d’un arbre. Une barre noire horyzontale est affichée, elle correspond à la classification la plus optimisée (la plus fiable et découpant la population en un nombre maximal de classes).
Pour faire la classification, il faut alors choisir le nombre de classes en cliquant sur le graphique au niveau du gain d’inertie souhaité (barre verticale) qui est lié au nombre de classes.
Le graphique suggère 4 classes (la barre horyzotale coupe la populations en 4 groupes). Pour notre exercice (classer les athletes), 3 classes suffiront (d’après les groupes identifiés lors de l’ACP). Nous allons alors cliquer juste en-dessous du niveau de gain d’inertie 1.0. Les 3 classes sont alors représentées par des rectangles de couleur.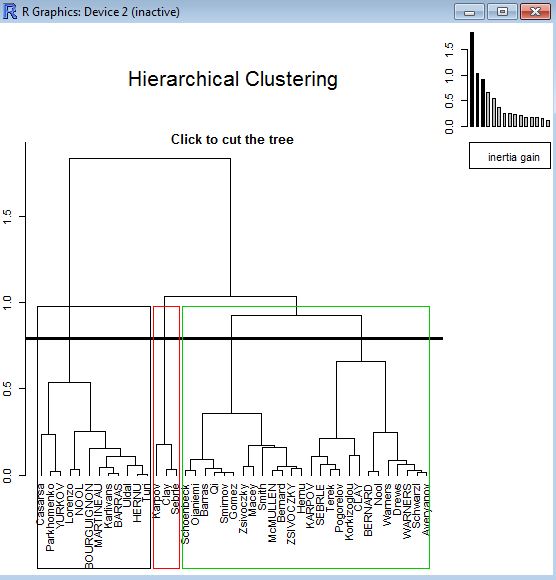
Analyse des resultats de la classification
Une fois, le nombre de classes choisis, les résultats sont affichés, ainsi que d’autres graphiques.
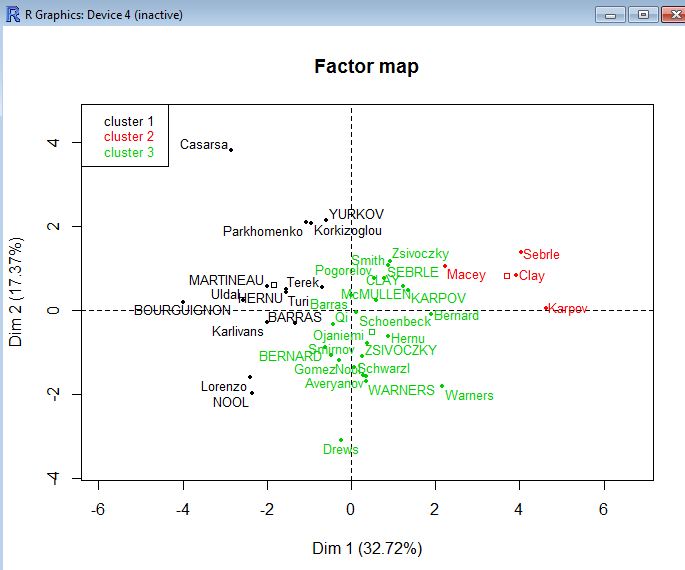
Le graphique des individus est généré en représentant chaque individu avec la couleur liée à sa classe. On observe ainsi nettement les 3 groupes d’athlètes de gauche à droite. Le barycentre (centre de gravité) de chaque classe est représentée par un petit rectangle de la couleur de la classe.
En reprenant les conclusions de l’ACP, il apparaissait que la dimension 1 décrivait le mieux la variable illustrative « points, ce qui traduit le fait que les athlètes bien positionnés sur cette dimension sont les meilleurs athlètes. Avec le graphique ci-dessous, on peut donc résumer la classification en disant que le groupe 1 est celui des athlètes les moins bons, le groupe 3 celui des athlètes moyens et le groupe 2 celui des meilleurs athlètes.
Parmi les tableaux affichés, on va avoir l’apport de chaque variable dans la classification et la description de chaque classe selon les variables, la même chose avec les dimensions, ainsi que la description des classes avec les individus extrêmes.
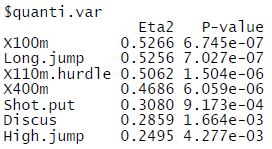
Le premier tableau concerne l’apport des variables à la classification. Cet apport est calculé selon la variance inter-groupes (inter-classes) expliquée par la variable. Ainsi, plus la valeur est grande pour Eta2, plus la variable explique les différences entre les classes. Et une p-value est associé à l’eta2 pour exprimer sa significativité.
Dans notre exemple, les variables X100m et Long.jump sont celles qui différencient le plus les groupes. C’est assez logique puisque sur les graphiques de l’ACP ces 2 variables sont celles qui décrivent le mieux la dimension 1 qui représente l’axe horyzontal. Et sur le graphique des individus, on constate que la classification suit l’axe horyzontal avec un groupe à droite, un groupe au centre et un autre à droite.
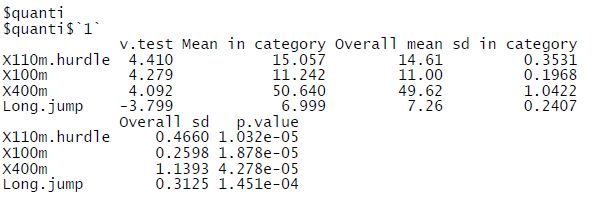
Chaque classe est ensuite décrite avec les variables la caractérisant. Ainsi, la classe 1 est décrite surtout par les variables X100m.hurdle, X100m, X400m et Long.jump.
Pour chacune des variables, une valeur est associée au vtest. Le vtest permet d’illustrer les valeurs des individus de la classe pour une variable comparé aux valeurs de la population. Ainsi, si une valeur est positive pour une variable, cela signifie que les individus de cette classe ont une valeur plus grande que ceux de la population. Ce v.test se base notamment sur la moyenne et la variance de la classe et de la population.
Pour la classe 1, les individus ont des valeurs plus importantes que la normale pour les variables X100m.hurdle, X100m et X400m, ce qui signifie qu’ils courent moins vite à ces épreuves. Les valeurs du vtest de ces variables sont proches, ce qui signifie que la différence avec la population est la même pour ces 3 variables. Et à l’inverse, la variable long.jump a une valeur négative, ce qui traduit le fait que les individus de cette classe sautent en general des distances plus courtes que les autres.
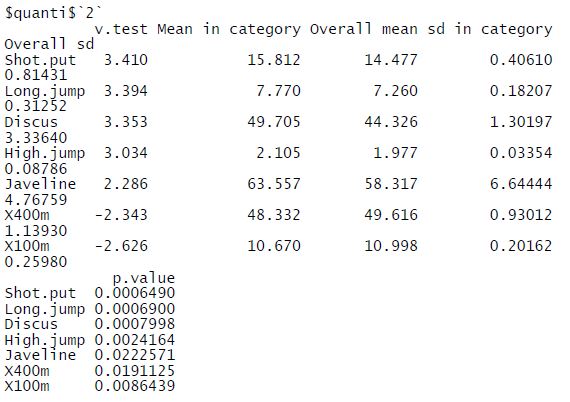
Ci-dessous le même tableau pour la classe 2. On remarque que les variables décrivant cette classe sont différentes.
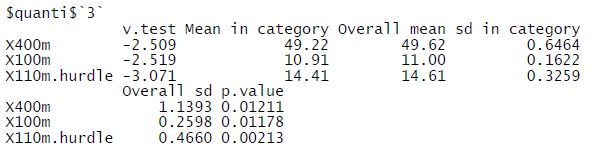
Pareil pour la classe 3 :
Ensuite ce sont les mêmes tableaux avec les dimensions à la place des variables.
Ainsi, les individus de la classe 1 a des valeurs plus importantes que les autres. Et plus faibles pour la dimension 2. En reprenant les résultats de l’ACP, on peut résumer en disant que les individus de la classe 1 sont ceux qui sont moins bons aux épreuves de vitesse, mais plus forts aux épreuves de puissance et de force.
Ces tableaux et valeurs peuvent servir pour classer de nouveaux individus selon leurs valeurs pour chaque variable.
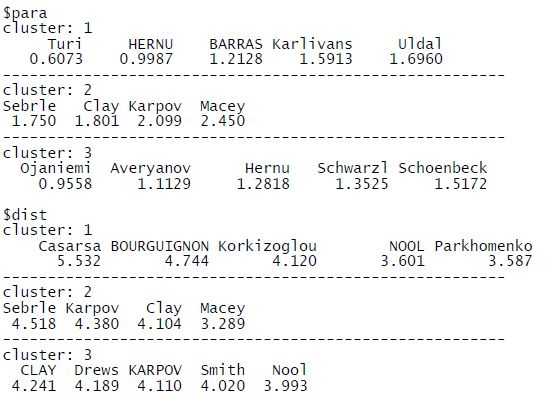
Et le dernier tableau décrit les classes/groupes en prenant les individus les plus caractéristiques. Ces individus sont sélectionnés selon leur proximité au centre de gravité de la classe ($para) et leur éloignement des centres de gravité des autres classes ($dist).
Ainsi, pour le groupe 1 (cluster 1), « Turi » est le plus proche du centre de gravité du groupe. Et Casarca est le plus éloigné des centres de gravité des groupes 2 et 3.
Pour + d’infos :