Pour expliquer des liens entre variables, on procède souvent à une régression linéaire qui va modéliser les liens entre une variable expliquée et les variables explicatives (qui permettent de l’expliquer).
Nous allons prendre comme exemple le dataset UScereal pour expliquer les valeurs en calories des céréales en fonction de leurs caractéristiques (graisse, fibres, potassium, sodium, proteines, sucres, etc). L’objectif est de trouver le modèle le plus précis avec le moins de variables explicatives.
Mise en place de la régression linéaire
Pour faire la régression linéaire, nous allons utiliser la fonction lm(variable expliquée ~ variables explicatives, données). Ainsi pour notre exemple nous allons générer le code suivant :
> data(UScereal, package = « MASS »)
> RegModel.1 <- lm(calories~carbo+fat+fibre+potassium+protein+shelf+sodium+sugars, data=UScereal) > summary(RegModel.1)
Avec Rcommander, après avoir chargé le set de données, la regression est réalisée en utilisant le menu Statistiques > Ajustement de modèles > Régression linéaire.
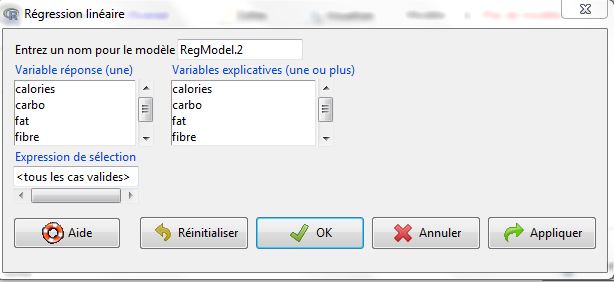
Une fenêtre s’affiche alors pour sélectionner la variable expliquée et les variables explicatives
Diagnostic de la régression
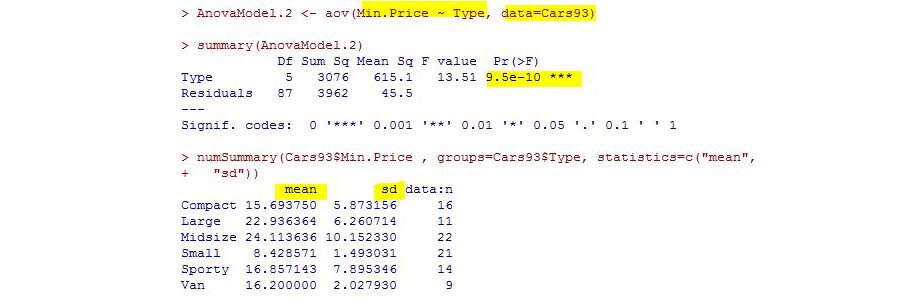
Les caractéristiques de la régression s’affiche alors avec la fonction summary().
Elle affiche notamment les coefficients de chaque variable explicative, la p-value associée (pour tester l’hypothèse où le coefficient est nul) et le coefficient de détermination (R2)
## Call:
## lm(formula = calories ~ carbo + fat + fibre + potassium +
protein +
## shelf + sodium + sugars, data = UScereal)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.92 -4.08 1.08 4.42 15.15
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -21.1591 3.7405 -5.66 5.5e-07 ***
## carbo 4.8699 0.1749 27.84 < 2e-16 ***
## fat 9.2741 0.7503 12.36 < 2e-16 ***
## fibre 2.8082 0.7188 3.91 0.00025 ***
## potassium -0.1159 0.0272 -4.27 7.8e-05 ***
## protein 4.8726 0.9791 4.98 6.5e-06 ***
## shelf 0.5668 1.3978 0.41 0.68667
## sodium 0.0121 0.0100 1.20 0.23368
## sugars 4.5434 0.2107 21.57 < 2e-16 *** ## — ## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1 ## ## Residual standard error: 7.95 on 56 degrees of freedom ## Multiple R-squared: 0.986, Adjusted R-squared: 0.984 On remarque que quasiment toutes les variables explicatives sont significatives (non nulles), sauf shelf et sodium. Fat semble être la variable explicative la plus importe, son coefficient est le plus grand. Et le coefficient de determination (Multiple R-squared) permet de juger de la force de la régression. R2 est compris entre 0 et 1 (comme les coefficient de corrélation) et représente le ratio de la variance expliquée par la régression sur la variance totale. Dans le cas d’une regression multiple (avec plusieurs variables), il y a le R2 ajusté qui corrige la tendance de R2 à augmenter avec le nombre de variables. Après avoir vu le résumé de la regression, il est possible d’avoir un apercu visuel de la regression. Pour cela, des graphiques de diagnostic peuvent être générés via le menu Modèles > Graphes > Diagnostic graphiques.
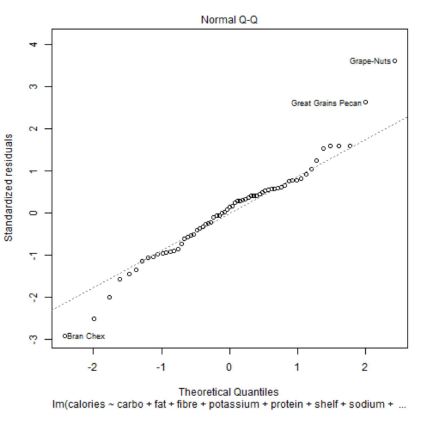
2 graphiques sont importants : le Q-Q plot et celui des distances de Cook
Le Q-Q plot permet de visualiser la distribution normale des résidus, ce qui valide les tests effectués à partir de la regression. Il compare la valeur des quartiles des résidus avec la valeur théorique (en cas de distribution normale).
Ci-dessus le Q-Q plot qui montre que les points suivent la transversale signe que les valeurs des résidus sont normalement distribuées.
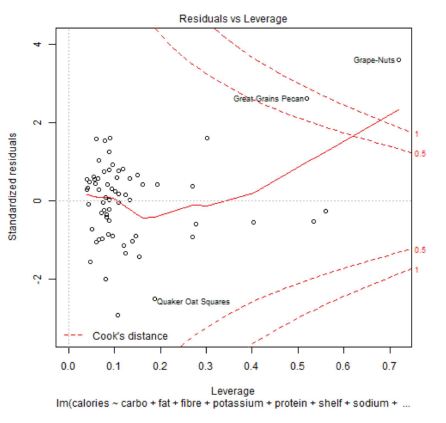
Le graphique des distances de Cook identifie les points extremes qui ont trop de poids dans la regression (ce sont les points dont la distance est supérieure à 1). Ces points sont identifiés à l’aide du leverage (l’influence d’un point sur les coefficients des variables) et la contribution au s2 (l’influence sur la variance des variables).
Ci-dessus le graphique des distances de Cook montre qu’une valeur au-delà de ligne « 1 » est à considérer comme extreme car il influence trop la régression. Il faut donc envisager à retirer cet individu du dataset utilisé pour le modèle (enlever cette valeur).
Sélection du meilleur modèle
Une fois, le diagnostic de la regression effectué, si le résultat est satisfaisant, il est possible de procéder à une optimisation de la regression.
L’optimisation va chercher la meilleure combinaison de variable afin de trouver le meilleur rapport entre la performance de la regression (variance expliquée) et le nombre de variables. Le but étant d’avoir le moins de variables pour expliquer le maximum d’informations.
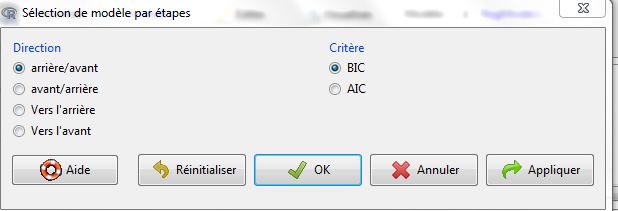
Pour cela, il est possible d’utiliser la méthode AIC (Akaike information criterion) ou BIC (Bayesian information criterion). Ces 2 méthodes sont relativement similaires, BIC pénalisant plus fortement le nombre de variables. Elles sont accessibles via le menu Modèles > Sélection de modèle par étapes.
La méthode calcule le coefficient BIC de la regression, puis il enlève la variable dont le coefficient BIC est inférieur à celui de la régression. Puis le coefficient BIC du nouveau modèle est calculé et une autre variable est enlevée jusqu’à ce qu’aucune variable n’ait un coefficient BIC inférieur à celui de la regression.
Le dernier modèle testé est donc le modèle sélectionné.
## Step: AIC=290.8
## calories ~ carbo + fat + fibre + potassium + protein + sugars
##
## Df Sum of Sq RSS AIC
## 3636 291
## + sodium 1 86 3550 293
## + shelf 1 4 3631 295
## – fibre 1 904 4540 301
## – potassium 1 1071 4707 303
## – protein 1 1562 5198 310
## – fat 1 9909 13545 372
## – sugars 1 30266 33902 432
## – carbo 1 56615 60251 469
##
## Call:
## lm(formula = calories ~ carbo + fat + fibre + potassium +
protein +
## sugars, data = UScereal)
##
## Coefficients:
## (Intercept) carbo fat fibre
potassium
## -19.608 4.937 9.311 2.691
-0.107
## protein sugars
## 4.850 4.568
Et pour confirmer le modèle sélectionné, il est possible de visualiser la meilleure combinaison de variables avec la sélection d’un sous-modèle via le menu Modèles > Sélection d’un sous-modèle.
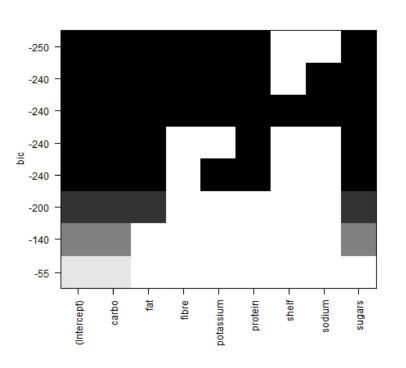
Un graphique s’affiche alors avec les variables sur l’axe horyzontal et le score du coefficient BIC sur l’axe vertical. Le meilleur sous-modèle est celui dont le score BIC est le plus élevé.
Dans l’image ci-dessus, le sous-modèle sélectionné est celui sans les variables shelf et sodium.
Pour + d’infos :
http://zoonek2.free.fr/UNIX/48_R_2004/11.html