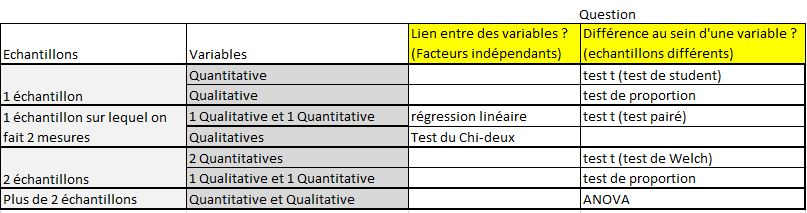
Pour comparer 2 échantillons, il est possible de réaliser un t-test. Nous allons voir les différentes façons de faire le test de Student avec ses variantes.
Le t-test teste l’hypothèse nulle qui veut que les moyennes des 2 échantillons soient égales (moyenne1=moyenne2). Il existe 2 facons de poser cette hypothèse nulle, soit en considérant que l’inégalité ne porte que sur un côté de la distribution normale (moyenne1>moyenne2), ce qu’on appelle one-tail test, soit en considérant que l’inégalité porte sur les 2 côtés (moyenne1<>moyenne2), ce qu’on appelle two-tail test. La différence entre le one-tail test et le two-tail test réside dans l’effet que l’on souhaite tester : si on cherche à savoir si l’effet d’un facteur est positif, en considérant que si la différence est négative c’est pareil qu’une égalité, alors le one-tail test convient.
Avant de réaliser un t-test
Il faut s’assurer que certaines conditions soient vérifiées :
- La distribution des échantillons suit une loi normale (courbe de Gauss). Pour cela, un test de normalité peut être effectué (par exemple Shapiro-Wilk test). Ou un Q-Q Plot peut être réalisé afin de juger de la normalité de la distribution. Sinon, il est possible de rendre des distributions compatibles à l’aide de la fonction logarithmique
- Les variances des échantillons sont homogènes (variances similaires). Pour cela, le test F de Fischer-Snedecor peut être utilisé
- A noter : le t-test de Student est relativement robuste et donne des résultats fiables, même si les 2 conditions ci-dessus ne sont pas vérifiés avec une grande assurance. Et ils sont adaptés à des échantillons de petite taille.
A noter : si on connait la variance de la population dont sont issus les échantillons, il est préférable de réaliser un z-test (au lieu d’un t-test). Et si il y a plus de 2 échantillons, il est préférable de faire une ANOVA (au lieu de plusieurs t-tests).
Le t-test pairé avec 2 mesures sur un même échantillon
Le t-test pairé correspond aux cas où les différentes mesures sont faites sur le même échantillon qui est donc utilisé 2 fois, d’où le terme d’échantillons dépendants. Ainsi, la taille des échantillons est la même. Lorsqu’on récolte les données, les lignes de la matrice de données correspondent aux différentes mesures pour un même individu de l’échantillon. Et il n’est pas possible de trier les données d’une colonne sans réorganiser simultanément les données des autres colonnes. Faute de quoi les résultats du test seront faussés, car le t-test pairé va étudier les différences de mesures pour chaque individu de l’échantillon.
Pour faire un t-test pairé, on part du principe que la variance de la population n’est pas connue. Et en préparant les données, il faut écarter les lignes où il y a des données manquantes (si il manque une des mesures d’un individu).
Ci-dessous, un exemple de t-test pairé avec Excel :
Ci-dessous le code correspondant à un t-test pairé avec R :
> t.test($sample1,$sample2,paired=TRUE)
Le t-test avec 2 échantillons indépendants
Ce test concerne des mesures faites sur 2 échantillons différents (avec des individus différents). Les lignes de la matrice de données peuvent être mises dans un ordre différent sans incidence sur le résultat. Les échantillons ne sont par conséquent pas forcément de même tailles (pas même nombre de lignes).
Pour faire un t-test avec des échantillons différents, on distingue 2 cas selon que l’on connaisse ou non la variance des populations. Si elles sont inconnues ou que les tailles des échantillons sont trop faibles pour l’estimer, on les considère comme inégales, on effectue alors la variante correspondant au test t de Welch.
Un exemple de t-test avec 2 échantillons indépendants avec excel :
Ci-dessous le code correspondant à un t-test avec 2 échantillons indépendants avec R :
> t.test($sample1,$sample2)
ou
> t.test($données~$facteur)
ou
> t.test($sample1,$sample2,var.equal=TRUE) si les variances sont égales
Le t-test avec 1 seul échantillon à comparer à une moyenne
Ce cas est similaire au t-test avec 2 échantillons indépendants. Sauf qu’ici, on ne dispose que d’un seul échantillon qu’on veut comparer à une moyenne (une référence donnée). Le t-test est donc réalisé comme si un deuxième échantillon existait avec la même valeur pour chaque individu (qui est la référence donnée).
Exemple de t-test avec 1 seul échantillon avec excel :
Ci-dessous le code correspondant à un t-test avec 1 seul échantillon à comparer à une moyenne avec R :
> t.test($sample,mu=$valeur-de-la-moyenne)
ou
> t.test($sample,mu=$valeur-de-la-moyenne,alternative= »less ») pour un one-tail test
Pour connaitre le résultat du test,
il faut regarder la p-value. Si elle est inférieure à 0,05, on rejette l’hypothèse nulle d’égalité des moyennes et on considère que les 2 échantillons sont différents.
Pour + d’infos :